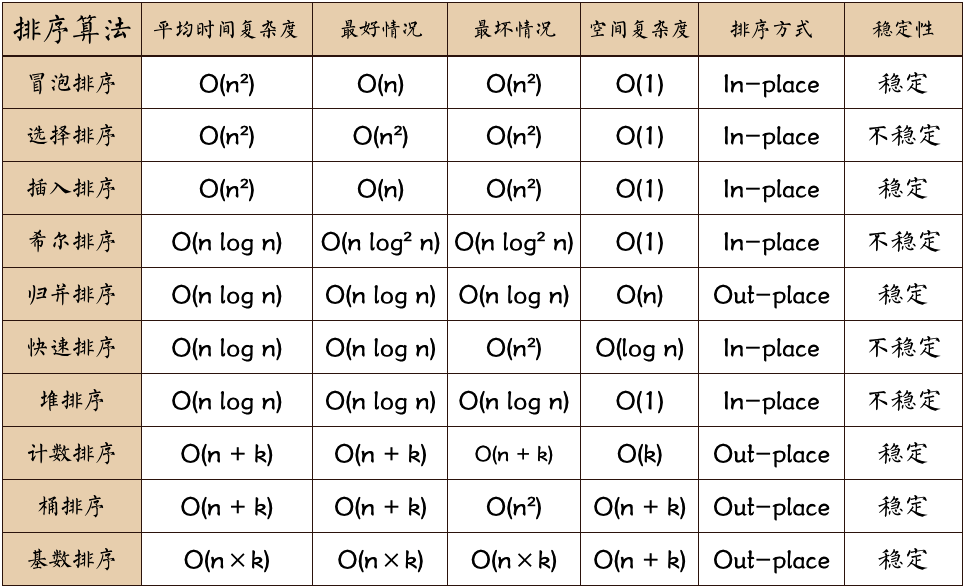
排序算法
冒泡排序
冒泡排序需要反复地遍历要排序的列表,比较相邻选项并交换它们,直到不需要交换为止。
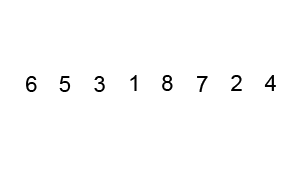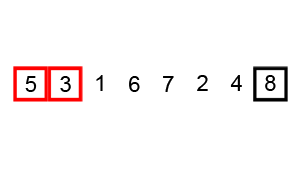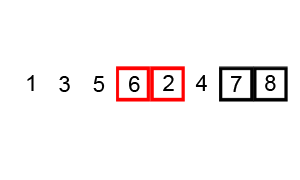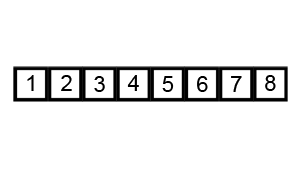
function bubbleSort(list) {
for (let i = 0; i < list.length - 1; i++) {
for (let j = 0; j < list.length - i - 1; j++) {
if (list[j] > list[j + 1]) {
;[list[j], list[j + 1]] = [list[j + 1], list[j]]
}
}
}
return list
}
冒泡排序是个比较简单但效率一般的算法,最坏情况下和平均的时间复杂度为 $O(n^2)$,这比许多排序算法的效率要低,甚至连同样复杂度为 $O(n^2)$ 的插入排序在多数情况下也比冒泡排序更快。因此,冒泡排序并不是一个实用的算法。
插入排序
插入排序的原理是通过构建有序序列,对于未排序的数据,在已排序的序列中从后向前扫描,找到相应位置并插入。
一般来说,插入排序采用 in-place 在数组上实现:
对于第一个元素,默认为已被排序;取出下一个元素,在已被排序的元素序列中从后向前扫描,直到找到已排序元素小于或等于新元素的位置并插入到该位置后,重复这样的操作直到所有元素都排序完成。
其实这很像玩扑克牌,每拿到一张牌,我们都要将新牌根据大小插入到合适的手牌的位置。
Notice
in-place 思想指的是不向系统申请内存以保证高性能。
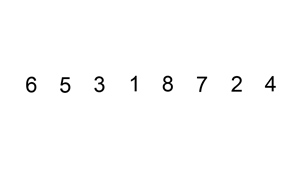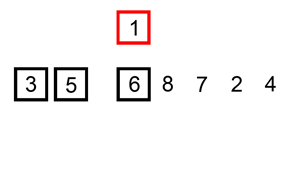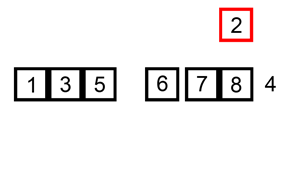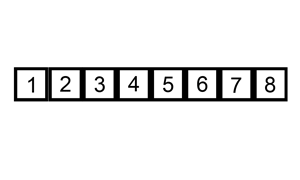
function insertionSort(list) {
const cpyList = [...list]
let len = cpyList.length
for (let i = 1; i < len; i++) {
const unSortItem = cpyList[i]
let j = i
for (; j > 0; j--) {
if (unSortItem >= cpyList[j - 1]) break
cpyList[j] = cpyList[j - 1]
}
cpyList[j] = unSortItem
}
return cpyList
}
插入排序的时间复杂度也是 $O(n^2)$,如果数组的大部分元素都按照顺序排列,使用插入排序是比较适合的,但插入排序不适合数据量比较庞大且混乱的数组。
鸡尾酒排序
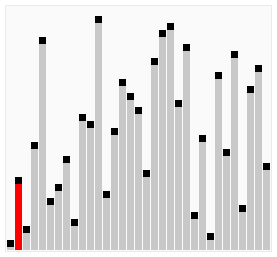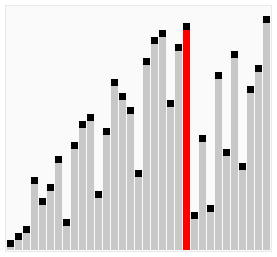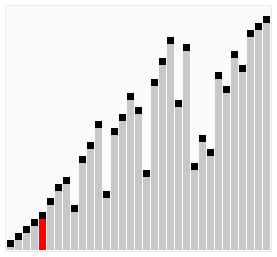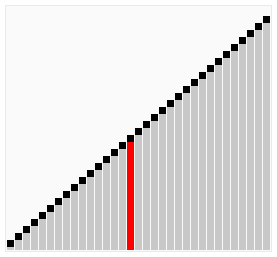
鸡尾酒排序相当于双向冒泡排序,也就是遍历顺序从低到高再从高到低,从低到高便利列表找出最大的元素放到最后,再从高到低找到最小的元素放到最左,然后依次类推。
这比冒泡排序要稍好一些,思考如下情况:
[2,3,4,5,1]
鸡尾酒排序只需要访问一次列表就可以完成排序,而冒泡排序需要 4 次,但在列表混乱的情况下,鸡尾酒和冒泡一样效率低。
function cocktailSort(list) {
const cpyList = [...list]
let left = 0
let right = cpyList.length - 1
while (left < right) {
for (let i = left; i < right; i++) {
if (cpyList[i] > cpyList[i + 1]) {
;[cpyList[i], cpyList[i + 1]] = [cpyList[i + 1], cpyList[i]]
}
}
right--
for (let i = right; i > left; i--) {
if (cpyList[i] < cpyList[i - 1]) {
;[cpyList[i], cpyList[i - 1]] = [cpyList[i - 1], cpyList[i]]
}
}
left++
}
return cpyList
}
可以看出,鸡尾酒排序的时间复杂度也是 $O(n^2)$,因此在大多数情况下仍然是效率较低的算法。
桶排序
桶排序指的先划分几个定量的范围,称为桶子,再将要排序的列表中的数据放到对应量的桶中,最后将每个非空桶中的元素排序(有可能要使用别的算法或以递归的方式继续使用桶排序进行排序),最后再把它们组合回列表。
先将数字放入对应桶中
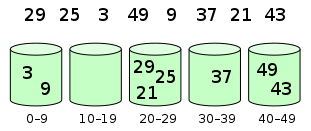
将桶中数字排序并拼接成新列表

function bucketSort(list, bucketsNum) {
const max = Math.max(...list)
const min = Math.min(...list)
const buckets = []
const bucketsSize = Math.floor((max - min) / bucketsNum) + 1
for (let i = 0; i < list.length; i++) {
const index = ~~(list[i] / bucketsSize)
let currentBucket = buckets[index]
!currentBucket && (currentBucket = [])
currentBucket.push(list[i])
let len = currentBucket.length
while (len > 1) {
if (currentBucket[len - 1] < currentBucket[len - 2]) {
;[currentBucket[len - 1], currentBucket[len - 2]] = [currentBucket[len - 2], currentBucket[len - 1]]
}
len--
}
buckets[index] = currentBucket
}
return buckets.flat(1)
}
Notice
~~ 双重非按位运算符用于截掉小数点后的数字,无论是正还是负,这与 Math.floor 有区别。
桶排序在最坏的情况下,空间复杂度将达到 $O(n^2)$,但平均复杂度为 $O(n+m)$(其中 n 为待排序元素个数,m 为桶的个数),在时间消耗上比较小,但在空间上的消耗就比较大了。
之所以说空间消耗大是因为如果列表中最大的元素为 10000,我们就需要一个长度为 10000 的数组来排序,这将白白的消耗大量的空间,有些不切实际;另外,如果桶的个数太多,那么 n+m 也可以是很大的。
桶排序需要的额外空间为 $O(m)$,待排序元素越均匀,也就是说,每个桶都可以被元素填的满满的,这种情况下桶排序可以发挥最大优势。
计数排序
计数排序的原理可以理解如下:
- 找出待排序数组中最大和最小的元素
- 统计数组中每个值为 i 的元素出现的次数,存入数组 C 的第 i 项
- 对所有的计数累加(从 C 中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素 i 放到数组的第 C[i] 项,没放一个元素 C[i] 就减去 1
可以这么说:假如有 10 个年龄不同的人,有 8 个人年龄比 A 小,那么 A 就排在第九位。
function countSort(list) {
const C = []
for (let i = 0; i < list.length; i++) {
const item = list[i]
C[item] >= 1 ? C[item]++ : (C[item] = 1)
}
const result = []
for (let j = 0; j < C.length; j++) {
if (C[j]) {
while (C[j] > 0) {
result.push(j)
C[j]--
}
}
}
return result
}
计数排序是用来排序 0~100 之间的数字的最好的算法,之所以这样说,是因为计数排序把元素本身映射成了数组下标,因此计数排序虽然不需要进行元素之间的比较,但在数组最大值比较大的时候的时候,会创建出范围很大的数组,比较浪费空间。
Notice
如果想要使用计数排序处理范围很大的数组,可以和基数排序相配合。
归并排序
归并排序是采用分治法的典型排序,指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。

Notice
在 CS 中,分治法基于多项分支递归的范型,字面理解为 “分而治之”,也就是把一个复杂的问题拆分成若干个相似的子问题,子问题可以直接使用简单方法解决,原问题的解即子问题的解的合并。
function mergeSort(list) {
const len = list.length
if (len < 2) return list
const mid = Math.floor(len / 2)
// 将数组分成均等的两半(在len为奇数情况下,left比right少一个元素)
const left = list.slice(0, mid)
const right = list.slice(mid)
return merge(mergeSort(left), mergeSort(right))
}
function merge(left, right) {
const result = []
while (left.length > 0 && right.length > 0) {
const item = left[0] < right[0] ? left.shift() : right.shift()
result.push(item)
}
return result.concat(left, right)
}
归并排序需要额外空间进行排序计算,因此不是原地排序算法,空间复杂度为 $O(n)$;时间复杂度为 $O(n log n)$。
归并排序对数组进行的拆分很像二分搜索,将数组对半拆分直到不能拆为止,在最坏的情况下需要进行 $log_2 n + 1$ 步,而之后又要对每个子列表的每个元素进行一遍检查,因此最后归并排序的时间复杂度就是 $O(n log n)$。
归并排序的缺点在于它需要一个与待排序列表同样大小的额外空间,因此不建议使用它来排序大型列表。
基数排序
基数排序也是一种非比较型排序算法,原理是将整数按照位数切割成不同的数字,然后按每个位数分别比较。
基数排序的实现步骤是这样的:将所有待比较的数值统一为同样的数位长度,数位较短的数前面补上 0,然后从最低位开始将数值放入数组对应下标的位置,再取数值中高一位的数进行排序,重复操作直到最高位也排好了序,这样排序就完成了。

function radixSort(list) {
// 找出最大的数以确定范围和循环次数
const max = Math.max(...list)
const tmpList = Array.from({ length: 10 }, () => [])
let m = 1
while (m < max) {
for (let i = 0; i < list.length; i++) {
const digit = ~~((list[i] % (m * 10)) / m) // 取数值的个位十位百位。。。数
tmpList[digit].push(list[i])
}
let index = 0
for (let i = 0; i < tmpList.length; i++) {
while (tmpList[i].length > 0) {
list[index++] = tmpList[i].shift()
}
}
m *= 10
}
}
基数排序的时间复杂度为 $O(k*n)$,n 是排序元素个数,k 是数字位数,在忽略 k 的情况下,时间复杂度为 $O(n)$;从理论上讲,基数排序在一些情况下是最快的稳定排序算法,但它的缺点是需要额外的空间以及对键的分类有要求,因此想要对除了整数,字符串外其他类型数据进行排序的话要做额外处理。
选择排序
选择排序非常直观简单,它是从待排序列表找出最大或最小的数放到列表最左端,接着在剩下的数里寻找最大或最小的数,放到已排序列表的末尾。
function selectionSort(list) {
const len = list.length
for (let i = 0; i < len - 1; i++) {
let min = i
for (let j = i + 1; j < len; j++) {
if (list[j] < list[min]) min = j
}
if (min !== i) {
;[list[min], list[i]] = [list[i], list[min]]
}
}
return list
}
选择排序的时间复杂度 $n^2$,不需要额外空间几乎是选择排序的唯一优点,很少有场合适用选择排序。
希尔排序
希尔排序是插入排序的改进版本,为什么要改进呢,主要有以下两个原因:
- 插入排序在对几乎已经排好数据的列表来说效率高
- 但插入排序在大多数情况下比较低效,因为每次只能将数据移动一位
希尔排序会优先比较距离较远的元素,让元素朝着目标位置前进一大步,再采取越来越小的步长进行排序,最后使用插入排序,这个时候列表基本上已经排好了。


function shellSort(list) {
const len = list.length
for (let gap = len >> 1; gap > 0; gap >>= 1) {
for (let i = gap; i < len; i++) {
let temp = list[i]
let j = i - gap
for (; j >= 0 && list[j] > temp; j -= gap) {
list[j + gap] = list[j]
}
list[j + gap] = temp
}
}
return list
}
希尔排序的最坏和最坏时间复杂度都为 $O(n log^2n)$,在使用合适步长且列表较小的条件下,希尔排序甚至可以比快速排序和堆排序还要快。
堆排序
听名字就知道堆排序是利用堆这个近似完全二叉树的结构,并且子节点的键值或索引总是小于(大于)它的父节点。
Notice
完全二叉树是效率极高的数据结构,叶子节点只能出现在最下层和次下层,并且最下边一层的节点都集中在该层的左边的若干位置的二叉树。
堆有大根堆和小根堆,大根堆每个节点的值都大于它的子节点的值,而小根堆则相反。
堆通常使用一维数组来实现,再数组起始位置为 0 的时候:
- 父节点 i 的左子节点在位置
2i+1 - 父节点 i 的右子节点在位置
2i+2 - 子节点 i 的父节点在位置
Math.floor((i-1)/2)
堆排序的流程如下:
- 将待排序的数组构造成一个大根堆,堆顶端的数是数组中最大的数
- 将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为 n-1
- 将剩余的 n-1 个数再构造成大根堆,再将顶端数与 n-1 位置的数交换,如此反复执行,便能得到有序数组

function heapSort(list) {
const len = list.length
// 初始化大顶堆,从第一个非叶子结点开始
for (let i = Math.floor(len / 2 - 1); i >= 0; i--) {
shiftDown(list, i, len)
}
// 排序,每一次for循环找出一个当前最大值,数组长度减一
for (let i = len - 1; i > 0; i--) {
;[list[0], list[i]] = [list[i], list[0]] // 根节点与最后一个节点交换
shiftDown(list, 0, i) // 从根节点开始调整,并且最后一个结点已经为当前最大值,不需要再参与比较,所以第三个参数为 i,即比较到最后一个结点前一个即可
}
return list
}
function shiftDown(list, i, len) {
let temp = list[i] // 当前父节点
for (let j = 2 * i + 1; j < len; j = 2 * j + 1) {
temp = list[i]
// 判断父节点下面的左子节点是不是大于右子节点
if (j + 1 < len && list[j] < list[j + 1]) j++
// 两个字节点较大的那个和父节点比较
if (temp < list[j]) {
;[list[i], list[j]] = [list[j], list[i]]
i = j
} else {
break
}
}
}
堆排序的时间复杂度为 $O(n log n)$,与归并和快速排序相同,而且只需要额外 $O(1)$ 的辅助空间,但在大多数情况下还是要比快速排序慢一些。
快速排序
快速排序就像它的名字一样,快速排序通常情况下明显比其他排序算法更快,至于最坏状况下的 $O(n^2)$ 次比较,是很少发生的。
快速排序的核心思想:
- 在待排序的元素任取一个元素作为基准(通常为第一个或中间一个)。
- 把比基准元素大的移到基准元素右边,小的移到左边。
- 对左右两个分块重复以上步骤直到所有元素都是有序的。
// 递归
function quickSort(list) {
const len = list.length
if (len < 2) return list
// 将第一个元素作为基准
const pivot = list.splice(0, 1)[0]
const left = []
const right = []
for (let i = 0; i < len - 1; i++) {
;(list[i] < pivot ? left : right).push(list[i])
}
return quickSort(left).concat(pivot, quickSort(right))
}
快速排序在大部分情况下时间复杂度为 $O(n log n)$,首先,由于我们要将数组不断地往下分割,因此需要的时间为 $O(log n)$,进行比较的时候又会将数组全部遍历一遍,需要的时间为 $O(n)$,所以快速排序的时间复杂度为 $O(n log n)$;在某些极端情况下,如:数组已经排过序,数组全部或大多数元素相同,这样的情况下,快速排序就和冒泡排序没有区别了,快速排序最坏的时间复杂度为 $O(n^2)$。
辅助信息
以上各算法复杂度信息一览