贪婪&动态规划
贪婪算法
贪婪算法,顾名思义就是每一步都选择最好的做法,用专业术语说, 如果每步都选择局部最优解,最终得到的就是全局最优解。这不禁让我想到了分治法:将复杂的大问题拆分成若干个简单的小问题去解决,合并它们的结果成为最优解。
贪婪算法通常以自顶向下的方式进行,每做出一次选择,问题就进一步简化,当问题不能再简化的时候停止。我们所熟知的迪杰斯特拉算法和广度优先算法都属于贪婪算法。
贪婪算法并不能解决所有问题,许多时候采用贪婪算法是很简单且迅速的,但无法保证能得到最优解。
(部分)背包问题
给定 n 个物品和一个容量为 C 的背包,物品 i 的重量是 Wi,其价值为 Vi,背包问题是如何选择入背包的物品,使得装入背包的物品的总价值最大,在部分背包问题中可以将物品的一部分装入背包,但不能重复装入。
由于可以选择部分物品,因此我们不用担心背包的空间被浪费,最合适的策略是优先选择性价比(价值/重量)最大的物品。

如上图,根据 4 样东西的价格和重量我们可以得出性价比:钻石>红宝石>金条=徽章。
因此我们优先拿走钻石和红宝石,剩下两点重量可以放一部分金条或徽章。
0/1 背包问题
题目来源于《算法图解》一书。
0/1 背包问题中的 0/1 指的是东西要么放进了背包,要么没有,不存在一半放进背包一般在外面的情况。
假设你是一个贪婪的小偷,背着可装 35 磅重东西的背包,在商场寻找机会偷窃各种物品。如何最大化利用背包空间并带走有价值的物品呢?
可偷窃商品如下:
| 商品名 | 价格(美元) | 重量(磅) |
|---|---|---|
| 音响 | 3000 | 30 |
| 笔记本电脑 | 2000 | 20 |
| 吉他 | 1500 | 15 |
我们可以尝试使用贪婪算法求解,按照贪婪算法的思想,我们应按照性价比的思想来决定优点拿走哪件物品。但显然三样东西性价比相同。如果选择先拿最贵的音响,那么剩下 5 磅重量就浪费了。
可如果我们偷的是笔记本电脑和吉他,我们不光充分利用的背包空间,还偷到了最多价值的物品(3500 美元)。
就算音响的价格改成 3499,性价比最高,但选择音响仍然不会是最优解。
因此,对于这个 0/1 背包问题,贪婪算法不能获得最优解,如果想要找出最优解,需要用到动态规划。
集合覆盖问题
集合覆盖就是要求出一个最小的集合,但可以覆盖全部的元素。
题目来源于《算法图解》一书。
假设你办了个广播节目,要让全美 50 个州的听众都收听得到。为此,你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用,因此你力图在尽可能少的广播台播出。现有广播台名单如下:
| 广播台 | 覆盖的州 |
|---|---|
| KONE | ID,NV,UT |
| KTWO | WA,ID,MT |
| KTHREE | OR,NV,CA |
| KFOUR | NV,UT |
| KFIVE | CA,ZA |
贪婪算法的重点就是要制定一个正确的贪婪策略,对于这个问题,我们可以优先选择覆盖最多未覆盖区域的电台。
const allOfLocations = ['ID', 'NV', 'UT', 'WA', 'MT', 'OR', 'CA', 'ZA']
const radioStationMap = {
// 广播台及其覆盖的州
KONE: ['ID', 'NV', 'UT'],
KTWO: ['WA', 'ID', 'MT'],
KTHREE: ['OR', 'NV', 'CA'],
KFOUR: ['NV', 'UT'],
KFIVE: ['CA', 'ZA'],
}
const neededStations = [] // 最终需要的电台列表
let coveredLocations = [] // 已选电台覆盖的州列表
function getUnion(listA, listB) {
// 求出两个列表的并集
return Array.from(new Set([...listA, ...listB]))
}
while (allOfLocations.length !== coveredLocations.length) {
let tmpStation = null // 当前进行测算的电台
let locations = null
let newCovered = null
for (let station in radioStationMap) {
locations = radioStationMap[station]
// 当前电台是否已经包含最终需要列表内了
if (neededStations.includes(station)) continue
// 求出当前电台覆盖州与已覆盖州的并集
const union = getUnion(coveredLocations, locations)
// 计算当前电台覆盖了多少未覆盖州
const uncoveredNum = union.length - coveredLocations.length
tmpStation = {
name: station,
num: uncoveredNum,
}
newCovered = union
}
if (tmpStation === null) break
neededStations.push(tmpStation.name)
coveredLocations = newCovered
}
求得:KTWO, KTHREE, KFOUR, KFIVE。
在这个问题中,贪婪算法的时间复杂度为 $O(n^2)$,其中 $n$ 为广播台数量。
旅行商问题
旅行商问题也是一个经典问题,假设有若干个城市,任何两个城市之间的都是确定的,旅行商从某一城市出发且必须经过所有城市,确定一条最短路线。
旅行商问题和集合覆盖问题有一个共同之处:你需要计算所有的解,并从中选出最小/最短的那个。这两个问题都属于 NP 完全问题。
Notice
NP 完全问题通常指以难解著称的问题,它可能有如下特征:
- 运行速度随着元素增加急剧降低。
- 涉及到所有组合。
- 不能将问题分成小问题,必须考虑所有可能情况。
- 问题涉及序列或集合且难以解决。
- 问题可以转换成集合覆盖或旅行商问题,它一定是 NP 完全问题。
对于这一类问题,贪婪算法无法确定求出的是不是最优解,只能是一个近似解,目前还没有任何方法可以快速解决这类问题。
实际上这类问题可以用多种算法解决,这里只说贪婪算法。贪婪算法求解过程为:从某一个城市开始,每此都选择离该城市最近的未旅行城市。
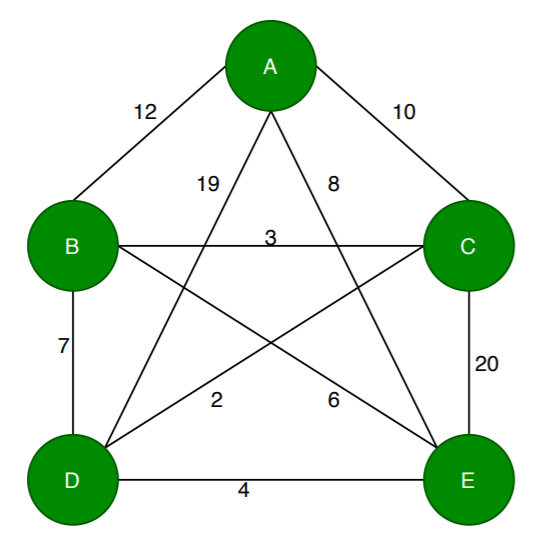
就拿上面这张图作为例子,我们来看看如果从任意一点开始走,能不能求得经过所有点的最短路径:
const cityNum = 5
// 存储5个城市到各个城市的距离
const routeMap = [
[0, 12, 10, 19, 8],
[12, 0, 3, 7, 6],
[10, 3, 0, 2, 20],
[19, 7, 2, 0, 4],
[8, 6, 20, 4, 0],
]
const randomNum = Math.floor(Math.random() * 5)
const beginCity = randomNum // 出发城市
const traveledCity = [randomNum] // 已经过城市列表
let sumGap = 0
let currentCity = randomNum // 当前所在城市
while (true) {
const currentCityRoute = routeMap[currentCity]
let nearestCity = null // 最近的城市
for (let j = 0; j <= cityNum - 1; j++) {
// 如果距离为0说明是当前城市
if (traveledCity.includes(j)) continue
// 如果最近城市未指定,则暂定为j
if (nearestCity === null) nearestCity = j
// 如果距离不是最短的,则更新最近城市
if (currentCityRoute[nearestCity] > currentCityRoute[j]) {
nearestCity = j
}
}
currentCity = nearestCity
sumGap += currentCityRoute[nearestCity]
traveledCity.push(nearestCity)
// 如果所有城市都已经旅行过,退出
if (traveledCity.length === cityNum) break
}
经过多次测试,所得出结果如下:
| 起始点 | 距离 | 经过点 |
|---|---|---|
| A | 17 | [A,E,D,C,B] |
| B | 17 | [B,C,D,E,A] |
| C | 24 | [C,D,E,B,A] |
| D | 19 | [D,C,B,E,A] |
| A | 21 | [E,D,C,B,A] |
可以看到从不同的城市出发,所求得的最短路径是不同的。
动态规划
动态规划在流程上与贪婪算法相反,先解决子问题,再逐步解决大问题。弗洛伊德最短路径算法就是采用动态规划的形式计算的。
我们先前说过,贪婪算法对于 0/1 背包问题是没有办法取得最优解的,但动态规划可以,来看看动态规划如何解决。
还是上面那道题,如何用 35 磅载重的书包带走最有价值的物品:
| 商品名 | 价格(美元) | 重量(磅) |
|---|---|---|
| 音响 | 3000 | 30 |
| 笔记本电脑 | 2000 | 20 |
| 吉他 | 1500 | 15 |
首先我们需要列出一个二维表,x 轴为背包容量,y 轴为可选择商品:
| 商品/背包容量 | 15 | 20 | 25 | 30 | 35 |
|---|---|---|---|---|---|
| 吉他 | |||||
| 音响 | |||||
| 笔记本电脑 |
Notice
你可能会疑惑为什么背包容量要从 15 开始排列到 35,因为动态规划是先从小问题着手的,进而解决大问题。
我们假设小偷暂时只能偷吉他,可以确定的是,表格里面所有容量的背包都可以装下吉他:
| 商品/背包容量 | 15 | 20 | 25 | 30 | 35 |
|---|---|---|---|---|---|
| 吉他 | 1500$ | 1500$ | 1500$ | 1500$ | 1500$ |
| 音响 | |||||
| 笔记本电脑 |
如果再加上音响呢?
| 商品/背包容量 | 15 | 20 | 25 | 30 | 35 |
|---|---|---|---|---|---|
| 吉他 | 1500$ | 1500$ | 1500$ | ||
| 音响 | 1500$ | 1500$ | 1500$ | 3000$ | 3000$ |
| 笔记本电脑 |
在背包容量小于 30 的时候,我们最多能拿走 1500 美元价值的吉他,但容量大于等于 30 的时候,我们就可以舍弃吉他,带走 3000 美元的音响!
如果考虑笔记本电脑呢?
| 商品/背包容量 | 15 | 20 | 25 | 30 | 35 |
|---|---|---|---|---|---|
| 吉他 | 1500$ | 1500$ | 1500$ | 1500$ | 1500$ |
| 音响 | 1500$ | 3000$ | |||
| 笔记本电脑 | 1500$ | 2000$ | 2000$ | 3000$ | 3500$ |
可以发现,背包容量为 20 的时候,我们最多可以带走 2000 美元的笔记本电脑。但在 35 容量的时候,我们可以同时带走吉他和笔记本电脑,因为我们在 15 磅和 20 磅的情况下可以分别带走 1500 美元和 2000 美元的物品。
但愿你已经明白什么是动态规划,现在让我们用代码实现一下:
function maxKnapsack(items, capacity) {
// 初始化二维数组
const result = Array.from({ length: items.length + 1 }, () => {
return Array.from({ length: capacity }, () => 0)
})
// 提取重量
let weights = items.map((item) => item.weight)
// 提取价格
let values = items.map((item) => item.value)
for (let i = 0; i < items.length + 1; i++) {
for (let j = 0; j < capacity + 1; j++) {
if (i === 0 || j === 0) {
result[i][j] = 0
} else if (weights[i - 1] <= j) {
let included = values[i - 1] + result[i - 1][j - weights[i - 1]]
let excluded = result[i - 1][j]
result[i][j] = Math.max(included, excluded)
} else {
result[i][j] = result[i - 1][j]
}
}
}
return result[items.length][capacity]
}
console.log(
maxKnapsack(
[
{ weight: 15, value: 1500 },
{ weight: 30, value: 3000 },
{ weight: 20, value: 2000 },
],
35
)
) // 3500
当你理解了动态规划算法,就可以知道动态规划算法会存储每一个小问题的答案(比如存储在二维数组),下个问题的答案通常需要参考上一个子问题的答案,并且不会因为题目的增长而导致速度的断崖式下降。
相比于动态规划,贪婪算法着重于只考虑眼前的情况,动态规划则考虑全面,避免了“鼠目寸光”。
优缺点比较
贪婪算法的优点:
- 在任何时候都只需要考虑一个子问题。
- 空间复杂度小。
- 在处理部分背包问题时十分优秀。
贪婪算法的缺点:
- 不能确定最优解。
- 只依靠上一步的结果推导下一步的解,每一步决策都无法改变。
动态规划的优点:
- 能够得到全局最优解。
- 在有很多重复问题的时候可以快速地得出答案。
动态规划的缺点:
- 不能处理部分背包问题,要么不拿,要拿就全部拿走。
- 没有统一的标准模型。
- 在问题量很大的时候具有很大的空间复杂度。
但动态规划同样有缺陷,比如不能处理部分背包问题,要么不拿,要拿就全部拿走。而贪婪算法可以很轻松地处理这种情况。