最短路径算法

Dijkstra（迪克斯彻）算法

学习了离散数学之后，我一直对 Djikstra 算法(求最短路径)非常感兴趣，我想能不能用 JS 实现最短路径的算法

假设一个无向图是这样的：

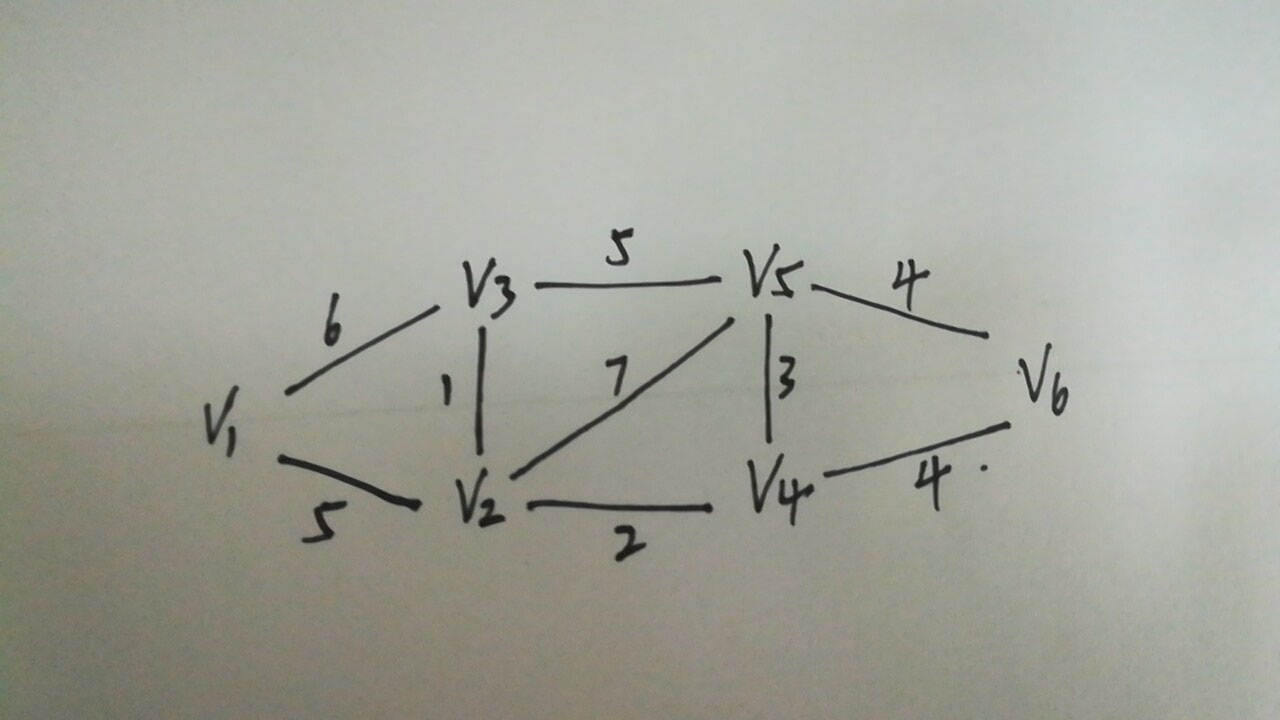
如何计算从 v1 至各个点的最短路径呢？

乍一眼看过去结果很明显，但在实际应用中往往比这张图复杂得多

为了获取图中的信息，我们需要先把上图转换为邻接矩阵：

截图未命名.jpg

这里 i 表示 infinite (无穷大)，表示两个点互不相连。

在 JS 中用二维数组表示矩阵：

const matrix = [
  [0, 5, 6, Infinity, Infinity, Infinity],
  [5, 0, 1, 2, 7, Infinity],
  [6, 1, 0, Infinity, 5, Infinity],
  [Infinity, 2, Infinity, 0, 3, 4],
  [Infinity, 7, 5, 3, 0, 4],
  [Infinity, Infinity, Infinity, 4, 4, 0],
]

获取顶点个数和行数：

const dots = matrix.length
const cols = matrix[0].length

检验邻接矩阵是否正确：

for (let item of matrix) {
  if (item.length !== dots) throw new Error('邻接矩阵数据错误')
}

声明一个长度为六的数组，并将其所有元素填充为 Infinity：

const finDistance = new Array(dots).fill(Infinity)

因为 v1 到 v1 距离为 0，所以把数组第一个元素设为 0：

finDistance[0] = 0

接下来就是最为重要的环节了，首先两点间的距离必须小于 Infinity才能够相连，需要比较起始点几个相连点之间的距离，选择最短距离的那个点相连：

for (let i = 0; i < dots; i++) {
  if (finDistance[i] < Infinity) {
    for (let j = 0; j < cols; j++) {
      if (matrix[i][j] + finDistance[i] < finDistance[j]) {
        finDistance[j] = matrix[i][j] + finDistance[i]
      }
    }
    console.log(finDistance)
  }
}

可以看到路径是如何一步一步推算出来的：

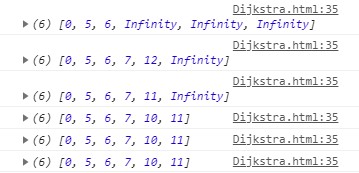
截图未命名.jpg

我们可以将其封装为一个函数方便使用：

function dijkstra(matrix, startDot = 0) {
  const dots = matrix.length
  const cols = matrix[0].length
  for (let item of matrix) {
    if (item.length !== dots || startDot > dots - 1) throw new Error('邻接矩阵数据错误')
  }
  const finDistance = new Array(dots).fill(Infinity)
  finDistance[startDot] = 0
  for (let i = 0; i < dots; i++) {
    if (finDistance[i] < Infinity) {
      for (let j = 0; j < cols; j++) {
        if (matrix[i][j] + finDistance[i] < finDistance[j]) {
          finDistance[j] = matrix[i][j] + finDistance[i]
        }
      }
    }
  }
  return finDistance
}

const matrix = [
  [0, 5, 6, Infinity, Infinity, Infinity],
  [5, 0, 1, 2, 7, Infinity],
  [6, 1, 0, Infinity, 5, Infinity],
  [Infinity, 2, Infinity, 0, 3, 4],
  [Infinity, 7, 5, 3, 0, 4],
  [Infinity, Infinity, Infinity, 4, 4, 0],
]

const shortest = dijkstra(matrix, 0)

Dijkstra 算法是一种贪心算法，它不能够计算带权为负的图，这是因为下一条路径都是由当前更短的路径衍生出来的路径，不存在回溯的过程，也就是说前面的路经定下来就不能够修改了。如果权值存在负数，有可能需要回溯才能找到更短的路径，这样不满足 Dijkstra 的机制

此算法时间复杂度为 O(N^2)

Floyd（弗洛伊德）算法

该算法的实现非常简洁，与 Dijkstra 算法类似，与之不同的是，Floyd算法用到了二重初始化和三重 for 循环

还是用上边的例子

const matrix = [
  [0, 5, 6, Infinity, Infinity, Infinity],
  [5, 0, 1, 2, 7, Infinity],
  [6, 1, 0, Infinity, 5, Infinity],
  [Infinity, 2, Infinity, 0, 3, 4],
  [Infinity, 7, 5, 3, 0, 4],
  [Infinity, Infinity, Infinity, 4, 4, 0],
]
let finDistance = floyd(matrix)
function floyd(matrix) {
  const dots = matrix.length
  for (let k = 0; k < dots; k++) {
    for (let i = 0; i < dots; i++) {
      for (let j = 0; j < dots; j++) {
        matrix[i][j] = Math.min(matrix[i][j], matrix[i][k] + matrix[k][j])
      }
    }
  }
  return matrix
}

Floyd 算法是一个采用动态规划思想的算法，这个算法看上去非常简单，只需要三重 for 循环加上一个判断大小的语句，一开始我非常怀疑这个算法的准确性，但事实证明，这个算法确实能够得到最短路径

这个算法涉及到三个点，假设 i 为起点，j 为终点，k 为中间点，那么要得到 i 到 j 的最短距离，首先要找到 i 到 k 的最短距离和 j 到 k 的最短距离。由于 k 是中间点，所以 k 的 for 循环一定要写在外面。这个算法的核心大概就是这样子的：

$1$

此算法时间复杂度为 O(N^3)

Bellman-Ford （贝尔曼-福特）算法

Bellman-Ford 算法是一种可以计算负权边的算法，但是他不能计算负权回路，负权回路指的是一个环上权值之和为负数，在这种情况下 Bellman-Ford 算法就会陷入死循环，为只要在负权回路上不断兜圈子，所得的最短路长度可以任意小。

一下面这幅图为例：

由于是有向图，我们需要知道路径的方向和权值：

const vertices = ['A', 'B', 'C', 'D'] //点
const edges = [
  //边，u表示起始点，v表示终点，w是权值
  { u: 'A', v: 'B', w: 4 },
  { u: 'A', v: 'C', w: 3 },
  { u: 'B', v: 'C', w: -2 },
  { u: 'B', v: 'D', w: 3 },
  { u: 'C', v: 'D', w: 3 },
]

我们可以定义一个 Graph 类用于初始化：

class Graph {
  constructor() {
    if (!(this instanceof Graph)) return new Graph() //防止重复创建实例
    this.nodes = [] //图的节点集
    this.edges = [] //图的边集
    this.table = new Map() //节点标识表
  }
}

在定义两个构造函数构建对象用来存放节点信息和边的信息：

function Node() {
  if (!(this instanceof Node)) return new Node()
  this.id = null
  this.data = null
}
function Edge() {
  if (!(this instanceof Edge)) return new Edge()
  this.u = null
  this.v = null
  this.w = null
}

在 Graph 中初始化节点和边：

initNodes(ns) {
  for (let id of ns) {
    let v = Node();
    v.id = id;
    this.table.set(id, v);
    this.nodes.push(v);
  }
}
initEdges(es) {
  for (let r of es) {
    let e = Edge();
    e.u = this.table.get(r.u);
    e.v = this.table.get(r.v);
    e.w = r.w;
    this.edges.push(e);
  }
}

初始化之后，需要初始化最短距离，默认为无穷大：

function BellmanFord(nodes, edges, startNode) {
  let distance = new Map() //存放从起点到任意节点的最短路径
  for (let v of nodes) {
    distance.set(v, Infinity)
  }
  distance.set(startNode, 0) //初始化起始点最短路径为0
}

然后需要对各个点进行松弛操作：

for (let i = 1, len = nodes.length - 1; i < len; i++) {
  for (let e of edges) {
    if (distance.get(e.u) + e.w < distance.get(e.v)) {
      distance.set(e.v, distance.get(e.u) + e.w)
    }
  }
}

由于 Bellman-Ford 算法不能计算负权环，所以我们要检测是不是有负权环的存在：

for (let e of edges) {
  if (distance.get(e.u) + e.w < distance.get(e.v)) return null //返回null表示包涵负权回路
}

完整代码：

class Graph {
  constructor() {
    if (!(this instanceof Graph)) return new Graph() //防止重复创建实例
    this.nodes = [] //图的节点集
    this.edges = [] //图的边集
    this.table = new Map() //节点标识表
  }
  initNodes(vs) {
    for (let id of vs) {
      let v = Node()
      v.id = id
      this.table.set(id, v)
      this.nodes.push(v)
    }
  }
  initEdges(es) {
    for (let r of es) {
      let e = Edge()
      e.u = this.table.get(r.u)
      e.v = this.table.get(r.v)
      e.w = r.w
      this.edges.push(e)
    }
  }
}
function Node() {
  if (!(this instanceof Node)) return new Node()
  this.id = null //用来标识节点
  this.data = null //节点数据
}
function Edge() {
  if (!(this instanceof Edge)) return new Edge()
  this.u = null
  this.v = null
  this.w = null
}
function BellmanFord(nodes, edges, source) {
  let distance = new Map() //用来记录从原节点 source 到某个节点的最短路径估计值
  // 第一步: 初始化图
  for (let v of nodes) {
    distance.set(v, Infinity) // 初始化最短估计距离 默认无穷大
  }
  distance.set(source, 0) // 将源节点的最短路径估计距离 初始化为0
  // 第二步: 重复松弛边
  for (let i = 1, len = nodes.length - 1; i < len; i++) {
    for (let e of edges) {
      if (distance.get(e.u) + e.w < distance.get(e.v)) {
        distance.set(e.v, distance.get(e.u) + e.w)
      }
    }
  }
  // 第三步: 检查是否有负权回路 第三步必须在第二步后面
  for (let e of edges) {
    if (distance.get(e.u) + e.w < distance.get(e.v)) return null //返回null表示包涵负权回路
  }
  return {
    distance: distance,
  }
}
const nodes = ['A', 'B', 'C', 'D'] //点
const edges = [
  //边，u表示起始点，v表示终点，w是权值
  { u: 'A', v: 'B', w: 4 },
  { u: 'A', v: 'C', w: 3 },
  { u: 'B', v: 'C', w: -2 },
  { u: 'B', v: 'D', w: 3 },
  { u: 'C', v: 'D', w: 3 },
]
const g = new Graph()
g.initNodes(nodes)
g.initEdges(edges)
const r = BellmanFord(g.nodes, g.edges, g.nodes[0])
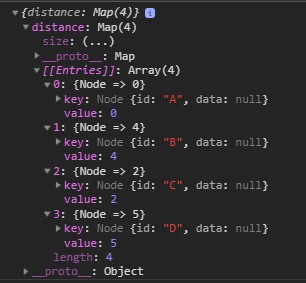
console.log(r)

控制台输出：

截图未命名.jpg

最短路径算法

Dijkstra（迪克斯彻）算法

Floyd（弗洛伊德）算法

Bellman-Ford （贝尔曼-福特） 算法

Bellman-Ford （贝尔曼-福特）算法