搜索算法

这里讨论下在列表中搜寻指定目标值的算法。

线性搜索(顺序搜索)

最差也是最简单的算法，按顺序从列表第一个元素开始查找比较，直到找到匹配项为止。

该算法在最坏的情况下时间复杂度为： $O(n)$，在假设列表每个元素匹配概率相等时，平均查找长度 ASL 为 $(n+1)/2$。

function linearSearch(list, matchVal) {
  for (let i = 0; i < list.length; i++) {
    if (list[i] === matchVal) return i
  }
}

二分搜索(折半搜索)

Notice

二分搜索的前提条件是列表必须为有序列表，因此在搜索前需要对列表进行排序。

先将需要匹配的值 k 与列表中间的数相比较(如果列表长度为偶数，则选择下标较小的元素作为中间元素)，中间元素将列表分成两个子列表，然后根据 k 与中间元素的比较的结果来选择对哪个子列表进行二分搜索。

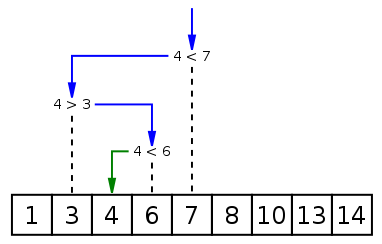
使用递归调用：

function binarySearch(list, matchVal, start, end) {
  if (start > end) return -1
  start = start || 0
  end = end || list.length
  const midIndex = Math.floor((start + end) / 2)
  const midVal = list[midIndex]
  if (midVal === matchVal) {
    return midIndex
  } else if (midVal < matchVal) {
    start = midIndex + 1
  } else {
    end = midIndex - 1
  }
  return binarySearch(list, matchVal, start, end)
}

推荐使用 while 循环方式：

function binarySearch(list, matchVal) {
  let start = 0
  let end = list.length - 1
  while (start <= end) {
    const midIndex = Math.floor((start + end) / 2)
    const mid = list[midIndex]
    if (matchVal === mid) {
      return midIndex
    } else if (matchVal < mid) {
      end = midIndex - 1
    } else {
      start = mid + 1
    }
  }
  return void 0
}

二分搜索算法的时间复杂度为 $O(log n)$，在最坏的情况下需要进行 $log_2 {n + 1}$ 次步骤后得到结果。

时间复杂度推算步骤：

设列表长度为 $n$，$f(n)$ 为得出结果所需步骤数。

第一次拆分：$f(n) = 1 + f(n/2)$。

第 s 次拆分：$f(n) = s + f(n/(s^2))$。

假如在第 s 次拆分之后，只剩下一个元素需要比较 $f(n) = s + f(1)$。

也就是 $n/{(s^2)} = 1$，$n = s^2$，$s = log2(n)$。

插值搜索

插值搜索基于二分搜索，也同样需要有序数组，对于插值搜索来说，比较适用于分布均匀的有序数组。

Notice

分部均匀可以理解为数组相邻元素之间的差值是一样或相近的。

在二分搜素中，对于中间点的计算如下：

midIndex = start + (start + end) / 2

而插值搜索改进了这个计算为：

midIndex = start + (matchVal - list[start]) / (list[end] - list[start]) * (end - start)

计算过程中依赖于列表两端的值，因此才适用于搜索均匀分布列表。

function insertionSearch(list, matchVal) {
  let start = 0
  let end = list.length - 1
  while (start <= end) {
    const midIndex = start + ((matchVal - list[start]) / (list[end] - list[start])) * (end - start)
    const mid = list[midIndex]
    if (mid === matchVal) return midIndex
    if (mid > matchVal) {
      end = midIndex - 1
    } else {
      start = midIndex + 1
    }
  }
  return void 0
}

插值搜索的时间复杂度为 $O(log(log n))$，在最坏情况下为 $O(n)$。

Notice

在数据量较大的情况下，插值搜索比二分搜索更快，但若该有序列表并不是均匀分布的，那情况可能会相反。

跳跃搜索(块搜索)

跳跃搜索类似于二分搜索，因此同样要求列表是有序的。

跳跃搜索会预先设置一个步长 gap，通过每次跳过一定个数的元素来检查更少的元素，这比线性搜索要效率更高。

gap 步长是需要进行计算的，如果数组长度为 n，那么在最坏的情况下需要进行 n/gap 次跳跃，如果在最后一次比较中，匹配元素值小于最后一个值，那么就要跳回前一个值进行 gap-1 次线性搜索，那么什么时候 n/gap + gap - 1 将取得最小值呢？在 gap 为 $\sqrt{n}$ 的时候，举个例子：

有如下长度为 10 的列表，我们想要搜索的元素是 128：

list = [1, 2, 4, 8, 16, 32, 64, 128, 256, 512]

跳跃搜索会将步长置为 Math.floor(Math.sqrt(10)) = 3。

将索引从 0 置为 3，再从 3 置为 6，再从 6 置为 9，这时发现 512 大于 128，因此索引从 9 跳回 6，开始进行线性搜索，进行两次对比后找到了 256。

function jumpSearch(list, matchVal) {
  const len = list.length
  const gap = Math.floor(Math.sqrt(len))
  let start = 0
  let end = gap
  while (list[Math.min(end, len) - 1] < matchVal) {
    start = end
    end += gap
    if (start > len) return false // 下一个起始索引已经超出数组，证明没有找到元素
  }
  let currentIndex = start
  while (currentIndex < Math.min(end, len)) {
    if (list[currentIndex] === matchVal) return currentIndex
    currentIndex++
  }
  return false
}

Notice

跳跃搜索的时间复杂度介于二分搜索和线性搜索之间，但如果我们要搜索的元素是很小或者是最小的元素，跳跃搜索的成本要比二分搜索小得多。

算法对比表

算法	平均时间复杂度	最坏时间复杂度	最优时间复杂度	空间复杂度	前置条件
线性搜索(顺序搜索)	$O(n/2)$	$O(n)$	$O(1)$	$O(1)$
二分搜索(折半搜索)	$O(log n)$	$O(log n)$	$O(1)$	迭代：$O(1)$，递归：$O(log n)$	数组有序
插值搜索	$O(log(log n))$	$O(n)$	$O(1)$	$O(1)$	数组有序且均匀分布
跳跃搜索(块搜索)	$O(\sqrt n)$	$O(\sqrt n)$	$O(1)$	$O(1)$	数组有序

搜索算法

线性搜索(顺序搜索)

二分搜索(折半搜索)

插值搜索

跳跃搜索(块搜索)

算法对比表

参考文章